Eksamenstid 5 timer
Del 1 (Uten hjelpemidler) skal leveres etter 2 timer.
Del 2 (Med hjelpemidler) skal leveres etter senest 5 timer.

DEL 1 – Uten hjelpemidler

Oppgave 1 (2 poeng)

 

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_01″]

Løs likningssettet

\(\large{ \begin{bmatrix}
5x+2y=4 \\
3x+4y=-6
\end{bmatrix}}\)

 

Oppgave 2 (1 poeng)

 

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_02″]

Løs likningen

\(\large{3 \cdot 10^x = 3000 }\)

 

Oppgave 3 (2 poeng)

 

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_03″]

Regn ut og skriv svaret på standardform

\(\huge{\frac{(0,5 \cdot 10^6)^2}{0,2 \cdot 10^{-4} + 3 \cdot 10^{-5}}}\)

 

Oppgave 4 (1 poeng)

 

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_04″]

Vis at

\(\large{\sqrt{15 } \cdot \sqrt{5} – \sqrt{48} = \sqrt{3} }\)

 

Oppgave 5 (2 poeng)

 

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_05″]

Regn ut og skriv svaret så enkelt som mulig

\(\large{\lg{1000} \cdot \lg{\sqrt[3]{10} \cdot \lg{\sqrt[5]{10^2}} \cdot \lg{0,00001}}}\)

 

Oppgave 6 (3 poeng)

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_06_ab”]

a) Vis at

\(x(x+2)(x-4) = x^3 – 2x^2 – 8x\)

b) Løs likningen

\(x^3-2x^2-8x=0\)

 

Oppgave 7 (2 poeng)

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_07″]

Løs ulikheten

\(x^2-2x-8 \geq 0\)

 

Oppgave 8 (3 poeng)

Funksjonen\(\small{ f }\)er gitt ved

\(\large{f(x)=x^2+kx+4}\)

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_08″]

For hvilke verdier av\(\small{ k}\) har grafen til \(\small{ f }\)

• ingen skjæringspunkter med x-aksen
• ett skjæringspunkt med x-aksen
• to skjæringspunkter med x-aksen

 

Oppgave 9 (3 poeng)

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_09_ab”]

a) Vis at

\(\huge{\frac{x+2+\frac{1}{x}}{\frac{x}{3} – \frac{1}{3x}} = \frac{3x^2+6x+3}{x^2-1}}\)

b) Skriv så enkelt som mulig

\(\huge{\frac{x+2+\frac{1}{x}}{\frac{x}{3} – \frac{1}{3x}}}\)

 

Oppgave 10 (4 poeng)

En funksjon \(\small{ f }\) er gitt ved

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_10_a”]

a) Bestem den gjennomsnittlige vekstfarten til i intervallet \(\small{f \in \left [ -2, 2 \right ]}\).

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_10_b”]

b) Bestem likningen for tangenten til grafen til \(\small{f}\) i punktet \(\small{ (1, f (1))}\).

 

Oppgave 11 (3 poeng)

Tenk deg at du kaster en rød og en blå terning.

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_11″]

Avgjør hvilket av de to alternativene nedenfor som er mest sannsynlig.

• Terningene viser samme antall øyne.
• Summen av antall øyne er 5 eller mindre.

 

Oppgave 12 (6 poeng)

 

I en likesidet trekant er alle sidene like lange og alle vinklene 60° . Høyden på en av sidene halverer denne siden.

Høyden deler den likesidete trekanten i to likestore rettvinklete trekanter.

I denne rettvinklete trekanten er vinklene 30° , 60° og 90° . I tillegg er hypotenusen dobbelt så
lang som den minste kateten.

Denne sammenhengen kalles 30° , 60° og 90° – setningen.

Ovenfor ser du to avsnitt fra en lærebok for 10. klasse.

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_12_a”]

a) Vis at \( \large{ DC = \frac{s\sqrt{3}}{2}}\)

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_12_b”]

b) Bruk \(\small{\Delta{ADC} }\) til å vise at \( \sin{60^{\circ}} = \frac{\sqrt{3}}{2}\).

I trekanten \(\small{PQR}\) er \( \small{PQ = 8}\) og \(\small{PR = 2 \sqrt{3} }\). Se skissen nedenfor.

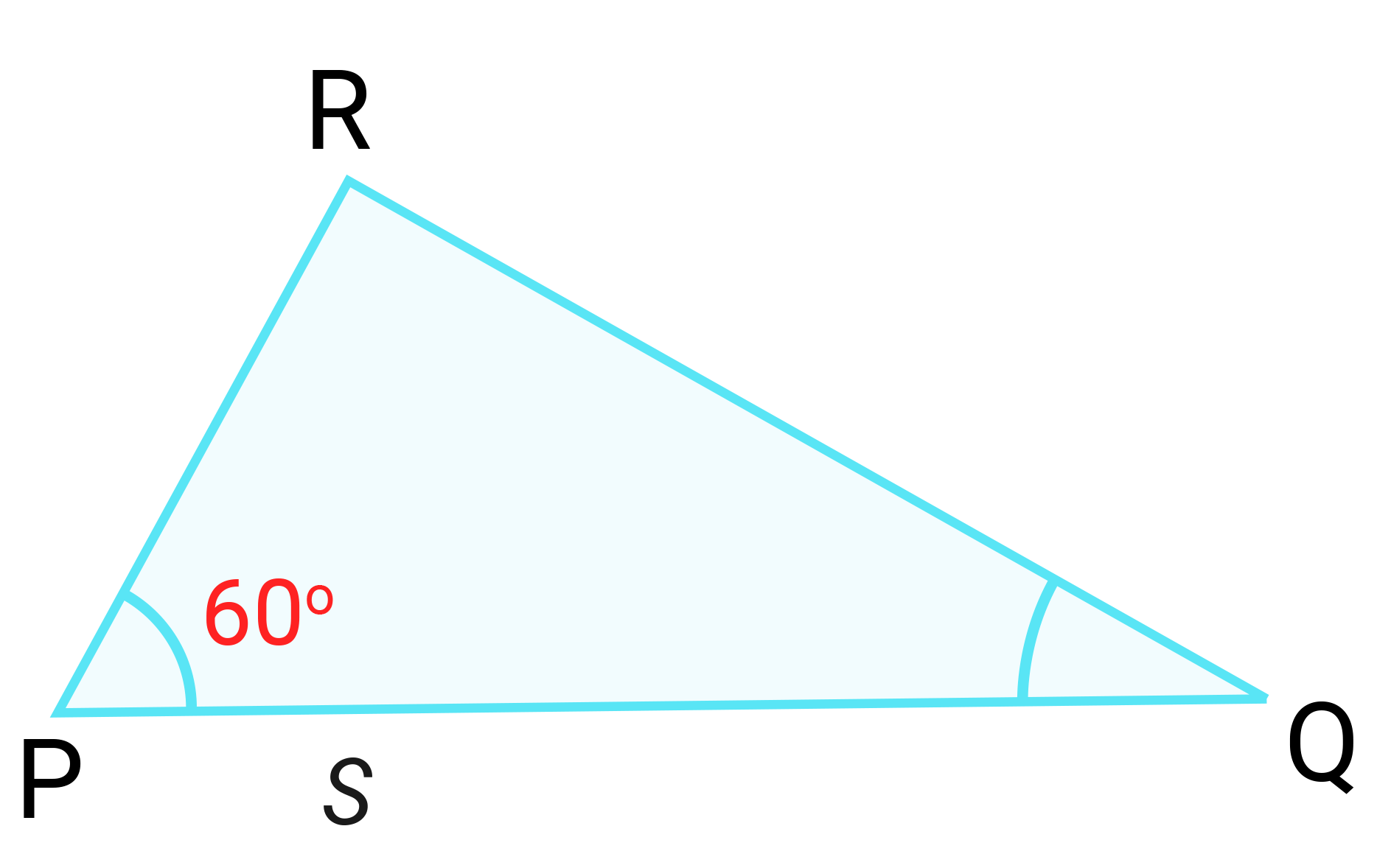
[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_12_c”]

c) Bestem arealet av \(\small{\Delta{PQR}}\).

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_12_d”]

d) Vis at \(\large{ \tan {Q} = \frac {3}{8- \sqrt{3}}}\)

 

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del1_13″]

Oppgave 13 (4 poeng)

 

Fire andregradsfunksjoner p , q , r og s er gitt ved

• \(\large{p(x) = x^2 – 2x}\)
• \(\large{q(x) = x^2 + 2x – 2}\)
• \(\large{r(x) = 4 – x^2}\)
• \(\large{s(x) = x^2 – 2x – 2}\)

Nedenfor ser du seks grafer.

Hvilken graf er grafen til p ?
Hvilken graf er grafen til q ?
Hvilken graf er grafen til r ?
Hvilken graf er grafen til s ?

Husk å begrunne svarene dine.

DEL 2 – Med hjelpemidler

 

Oppgave 1 (6 poeng)

 

Tabellen ovenfor viser hvor mye en kroneis kostet noen utvalgte år i perioden fra 1970 til
2017.

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del2_01_a”]

a) Legg opplysningene i tabellen ovenfor inn som punkter i et koordinatsystem der x-aksen viser antall år etter 1970 og y-aksen viser pris (kroner).

Funksjonen f er gitt ved

\( \space\ \space\ f(x)=0,0054x^2 + 0,26x + 0,9 \space\ \space\ , \space\ \space\ x \in \large{\left [ 0,50 \right ]} \)

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del2_01_b”]

b) Tegn grafen til \(\small{f}\) i samme koordinatsystem som du brukte i oppgave a).

I resten av denne oppgaven skal du bruke funksjonen \(\small{f}\) som en modell som viser prisen
\(\small{f(x)}\) kroner for en kroneis \(\small{x}\) år etter 1970.

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del2_01_c”]

c) Når var prisen for en kroneis 16 kroner, ifølge modellen?

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del2_01_d”]

d) Hvor mye har prisen for en kroneis i gjennomsnitt steget med per år fra 1975 til 2015?

 

Oppgave 2 (4 poeng)

 

Ved en videregående skole er det 640 elever. I en undersøkelse ble elevene spurt om når de legger seg kvelden før en skoledag.

• \(\large{\frac{1}{4}}\) av elevene svarte at de legger seg før klokka 23.

Det viser seg at

• \(\large{\frac{4}{5}}\) av elevene som legger seg før klokka 23, har et karaktersnitt over fire
• \(\large{\frac{1}{3}}\) av elevene som legger seg etter klokka 23, har et karaktersnitt over fire

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del2_02_a”]

a) Lag en krysstabell som illustrerer opplysningene som er gitt ovenfor.

Tenk deg at vi trekker ut en elev ved skolen tilfeldig.

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del2_02_b”]

b) Bestem sannsynligheten for at eleven har et karaktersnitt over fire.

Tenk deg at den eleven vi trakk i oppgave b), har et karaktersnitt over fire.

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del2_02_c”]

c) Bestem sannsynligheten for at denne eleven legger seg før klokka 23 kvelden før en skoledag.

 

Oppgave 3 (2 poeng)

 

Gitt trekanten ovenfor.

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del2_03″]

Bruk CAS til å bestemme s .

 

Oppgave 4 (6 poeng)

 

Figuren ovenfor viser to rettvinklete trekanter, \(\small{\Delta{ADC}}\) og \(\small{\Delta{DBC}}\). \(\small{AC = a}\), \(\small{BC = b}\). \(\small{AD = c_{1}}\), \(\small{CD = h}\), hvor \(\small{h}\) er høyden fra \(\small{C}\) på \(\small{AB}\). Maria påstår at høyden \(\small{h}\) kan uttrykkes på ulike måter:

• 1) \(h=a \cdot \cos{u}\)
• 2) \(h = b \cdot \cos{v}\)

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del2_04_a”]

a) Vis at Maria har rett

For å bestemme arealet \(\small{T}\) av \(\small{\Delta{ABC}}\) vil Maria regne slik: \(\large{ T = \frac{c_{1} \cdot h}{2} + \frac{c_{2} \cdot h}{2}}\)

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del2_04_b”]

b) Bruk blant annet resultatet fra oppgave a), og vis at dette uttrykket for arealet kan skrives som

\( \space\ \space\ \space\ \huge{T=\frac{a \cdot \sin{u} \cdot b \cdot \cos{v}}{2} + \frac{b \cdot \sin{v} \cdot a \cdot \cos{u}}{2}}\)

Mats bruker arealsetningen og får at arealet av trekanten også kan skrives slik:

\( \space\ \space\ \space\ \huge{T=\frac{1}{2}a \cdot b \cdot \sin{(u + v)}}\)

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del2_04_c”]

c) Bruk dette uttrykket og uttrykket du har for arealet fra oppgave b), til å vise at

\( \space\ \space\ \space\ \Large{\sin{u+v} = \sin{u} \cdot \cos{v} + \sin{v} \cdot \cos{u}}\)

 

Oppgave 5 (6 poeng)

 

En funksjon f er gitt ved

\( \space\ \space\ \space\ \Large{f(x)=x^2 – 6x + 8}\)

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del2_05_a”]

a) Vis at tangeten til grafen til \(\small{f}\) i punktet \((4, f(4))\) er parallell med linjen som går gjennom punktet \((2, f(2))\) og \((6, f(6))\).

Nedenfor ser du grafen til en funksjon \(\small{g}\) gitt ved

\( \space\ \space\ \space\ \Large{g(x)=ax^2 + bx + c \space\ \space\ , \space\ \space\ a \neq 0}\)

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del2_05_b”]

b) Bruk CAS til å bestemme stigningstallet til tangenten til grafen til g i punktet

\( \space\ \space\ \space\ \Large{M \left (\frac{p+q}{2}, g(\frac{p+q}{2}) \right )}\)

[mattevideo type=”eksamen” youtube=”KNAX6UE0qdM” amazon=”1t_eksv18_del2_05_c”]

c) Vis at linjen gjennom punktene P(p,g(p)) og Q(q,g(q)) er parallell med tangenten i oppgave b).